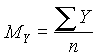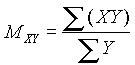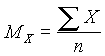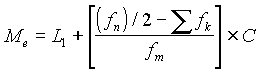Cuando se dispone de un gran número de datos, es conveniente ordenarlos en clases, según sus amplitudes sean iguales o diferentes. La tabla con los datos distribuidos en clases es llamada distribución de frecuencias o tabla de frecuencias.
Hay reglas empíricas que dan el número de clases que se debe utilizar, según el número total de datos disponibles. Se designa como amplitud de cada clase a la diferencia entre los valores máximo y mínimo de los datos, dividido por el número de clases utilizadas.
El concepto de distribución de frecuencias se ilustra mediante el Cuadro 5.1. el cual muestra la distribución de salarios de 97 trabajadores de la industria del cemento en un país centroamericano en el año 1968.
En los cálculos se suelen considerar los datos como si estuviesen concentrados en los centros de las clases. Los centros de clases son las medias aritméticas de los extremos de cada clase.
Representando gráficamente la tabla de frecuencias; se pueden observar con mayor claridad algunas características de la masa de los datos. La Figura 5.1. representa la tabla de frecuencia de la Tabla 5.1. y se denomina histograma. La línea quebrada que une los puntos medios de los lados superiores de los rectángulos recibe el nombre de polígono de frecuencias.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
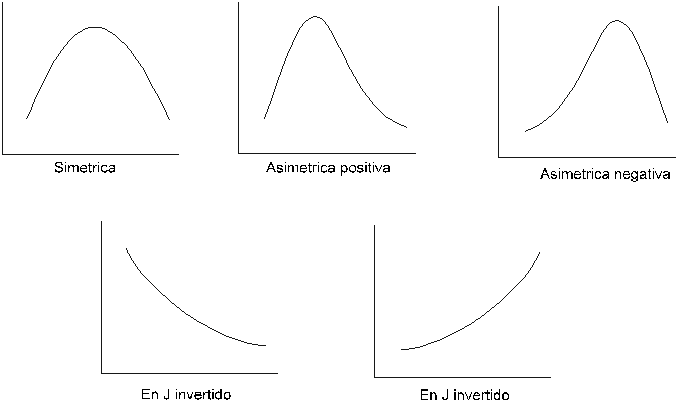
Figura 5.2